How to Determine Which Stat Regression Model Is Best
The mean model which uses the mean for every predicted value generally would be used if there were no informative predictor variables. Unfortunately this can be a huge number of possible models.
2 1 What Is Simple Linear Regression Stat 462
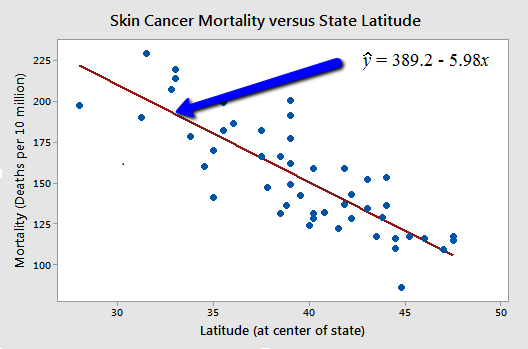
For our example both statistics suggest that North is the most important variable in the regression model.

. Statistical Methods for Finding the Best Regression Model The adjusted R squared increases only if the new term improves the model more than would be expected by chance and it. This connection is in the straight line linear regression which is best to estimate a single data point. A ΔBIC of greater than 10 means the evidence favoring our best model vs.
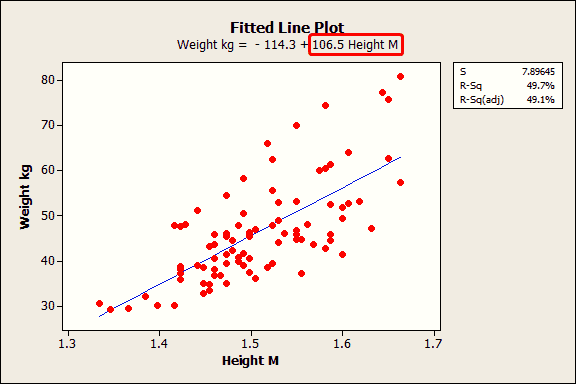
Now first calculate the intercept and slope for the regression. Statistical methods for finding the best regression model. The R² value also known as coefficient of determination tells us how much the predicted data denoted by y_hat explains the actual data denoted by y.
B the slope. What Statistical Rules to look for. It measures the distances called errors or variance of the residuals from the points to the regression line and squares them to remove any negative signs.
The fit of a proposed regression model should therefore be better than the fit of the mean model. Statistical measures can show the relative importance of the different predictor variables. The alternate is very.
If its between 6 and 10 the evidence for the best model and against the weaker model is strong. It is called multiple linerar regression. This is a hotly debated question.
The linear in linear regression only means linearity in the parameters. AIC weights the ability of the model to predict the observed data against. We can run plot incomehappinesslm to check whether the observed data meets our model assumptions.
First identify all of the possible regression models derived from all of the possible combinations of the candidate predictors. A regression analysis utilizing the best subsets regression procedure involves the following steps. Where ŷ is the predicted value of the response variable b 0 is the y-intercept b 1 is the regression coefficient and x is the value of the predictor variable.
Here we will discuss four of the most popular metrics. Besides obvious choices like prior non-linear transformations of predictor or outcome variables non-linear relationships can often be modeled flexibly by restricted cubic splines with parameters estimated in a linear regression model. For a good regression model you want to include the variables that you are specifically testing along with other variables that affect the response in order to avoid biased results.
Instead of y α β x ϵ you now have y α β 1 x 1. A well-fitting regression model results in predicted values close to the observed data values. Check the p-value for the terms in the model to make sure they are statistically significant and apply process knowledge to evaluate practical significance.
In other words it represents the strength of the fit however it does not say anything about the model itself it. Regression focuses on a set of random variables and tries to explain and analyze the mathematical connection between those variables. To determine which model is best examine the plot and the goodness-of-fit statistics.
U the regression residual. ŷ b 0 b 1 x. The Akaike information criterion is one of the most common methods of model selection.
So theres a good chance that. B 5 10620614 51989 62833 5 8801746 51989 2. If you do not know any modeling start with regression as it is most basic.
R-Squared R² y dependent variable values y_hat predicted values from model y_bar the mean of y. For the sake of example suppose we have three. Using linear regression we can find the line that best fits our data.
The predicted R-squared is a form of cross-validation and it can also decrease. Par mfrowc 22 plot incomehappinesslm par mfrowc 11 Note that the par mfrow command will divide the Plots window into the number of rows and columns specified in the brackets. Caveats for Using Statistics to Identify Important Variables.
In Minitab best subsets regression uses the maximum R 2 criterion to select likely models. Moreover it can explain how changes in one variable can be used to. In this example the line of best fit is.
Open the sample data ThermalEnergyTestMTW. A 62833 8801746 51989 10620614 5 8801746 51989 2. If you cant obtain a good fit using linear regression then try a nonlinear model because it can fit a wider variety of curves.
Regression analysis process is primarily used to explain relationships between variables and help us build a predictive model. Cross-validation determines how well. Lets now input the values in the regression formula to get regression.
The basic approach is to go with the smallest subset that fulfills certain statistical rules. Minitab Statistical Software offers statistical measures and procedures that help you specify your regression model. However these measures cant determine whether the variables are important in a practical sense.
My advice is to fit a model using linear regression first and then determine whether the linear model provides an adequate fit by checking the residual plots. The formula for this line of best fit is written as. The Statistics R squared adjusted R squared predicted R squared Mallows Cp and s Square root of MSE can be used to compare the results and these statistics are generated by the best subset procedure.
A good regression model is one where the difference between the actual or observed values and predicted values for the selected model is small and unbiased for train validation and test data sets. The Root Mean Squared Errors RMSE takes the square root of MSE and indicates the absolute fit of the model to the datahow close the observed data points are to the models predicted values. In statistics model selection is a process researchers use to compare the relative value of different statistical models and determine which one is the best fit for the observed data.
A the intercept. To measure the performance of your regression model some statistical metrics are used. β n x n ϵ where n represents the number of predictors covariates in your model.

Making Predictions With Regression Analysis Statistics By Jim
2 1 What Is Simple Linear Regression Stat 462
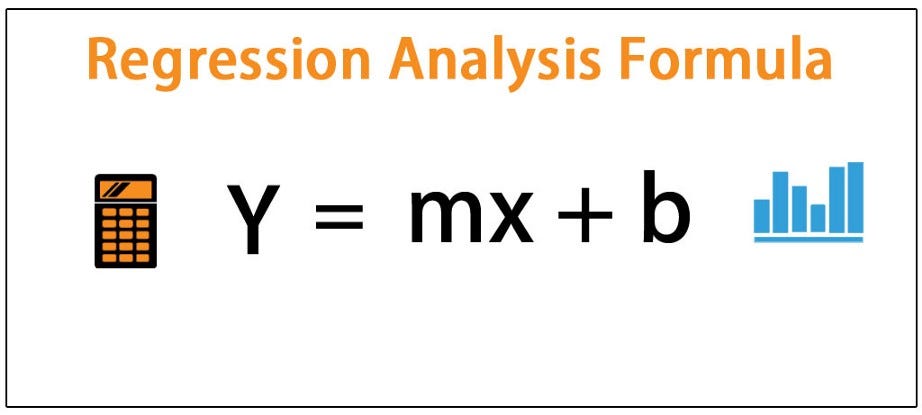
Step By Step Regression Analysis What Is Regression Analysis By Great Learning Medium

How To Choose Between Linear And Nonlinear Regression Statistics By Jim
How To Interpret P Values And Coefficients In Regression Analysis Statistics By Jim

Comparing Regression Lines With Hypothesis Tests Statistics By Jim

Ordinary Least Squares Regression Ols Statistical Software For Excel
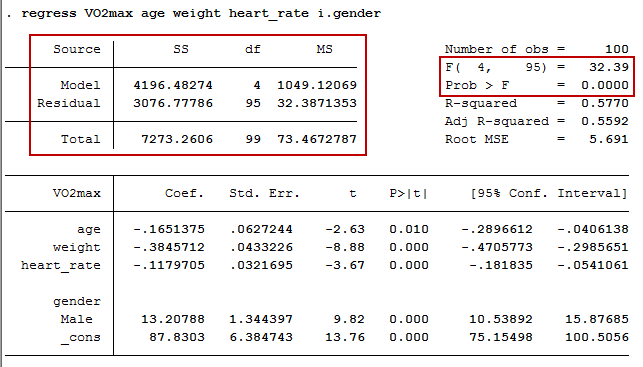
How To Perform A Multiple Regression Analysis In Stata Laerd Statistics

What Is The Regression Equation Magoosh Statistics Blog
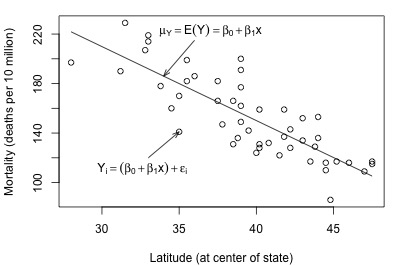
5 6 The General Linear F Test Stat 462
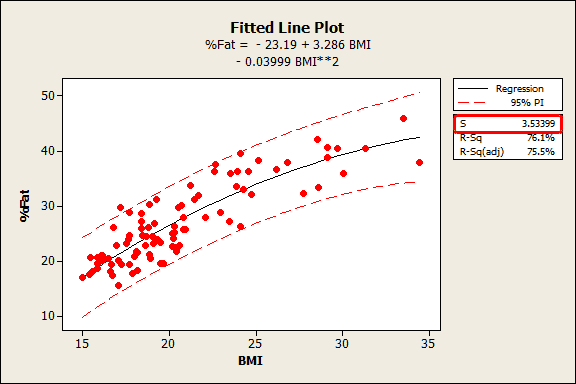
Regression Analysis How To Interpret S The Standard Error Of The Regression
Step By Step Regression Analysis What Is Regression Analysis By Great Learning Medium

Linear Regression Explained A High Level Overview Of Linear By Jason Wong Towards Data Science

How To Interpret Regression Models That Have Significant Variables But A Low R Squared Statistics By Jim

Comparing Regression Lines With Hypothesis Tests Statistics By Jim
Linear Regression Excel Step By Step Instructions

Generating Simple Linear Regression Results
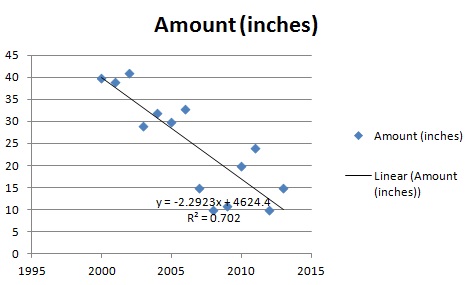
Regression Analysis Step By Step Articles Videos Simple Definitions
Comments
Post a Comment